Quarter-Tone Harmony/Harmonic Basis
The quarter-tone system also provides certain advantages from an acoustic standpoint, despite the system's dissonant reputation among composers.
Harmonic Series
The harmonic series is a series of pitches that occur naturally within common instruments and soundwaves, and it consists of all harmonics or overtones of any given pitch. Mathematically, the harmonic series of a frequency consists of all frequencies that are integer multiples of , or all where .
- String players and guitarists can play harmonics by lightly touching a string such that the string naturally vibrates in halves, thirds, fourths, etc., producing the harmonic series.
- Brass players know harmonics as "partials;" they can move their lips or change their embouchure to access different harmonics of a harmonic series, allowing them to play a wide range of pitches with only three or four valves.
The harmonic series and the intervals within it are very significant to Western harmony since Western melodic instruments heavily feature the harmonic series in some form in their overtone series.
Just intonation is the practice of tuning intervals the way they appear in the harmonic series; that is, by strict frequency ratios, such as 3:2 (perfect fifth), 5:4 (major third), 2:1 (octave), etc. However, just intonation was historically abandoned as music became more complex and instruments could not accommodate.
The Eleventh Harmonic
The first ten harmonics are reasonably approximated by the conventional system, although the seventh harmonic is very inaccurate:
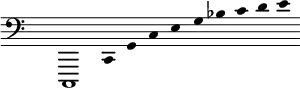
However, the eleventh harmonic cannot be properly approximated with the conventional system. Theorists and composers in the past have used either of the pitches F or F♯, which are equally inaccurate. The eleventh harmonic is, however, very accurately approximated with the quartertonal note F![]() .
.
Natural Horns
As Wyschnegradsky states in his Manual:
It is interesting to note that we have occasion to hear the eleventh harmonic each time natural horns or trumpets are given the fourth degree of the major scale. Since these instruments do not possess any tones other than that of the harmonic series, and the fourth degree of the major scale (the fifth below the fundamental) does not enter in the harmonic series, they must replace it with the eleventh harmonic.
He cites such an example:
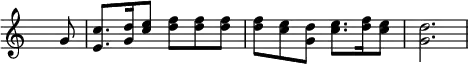
If this passage were to be played by natural horns, the players would be forced to replace all occurences of the note F with F![]() , the approximate eleventh harmonic of the C to which the horns are tuned:
, the approximate eleventh harmonic of the C to which the horns are tuned:
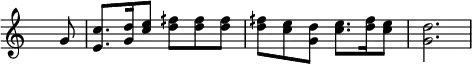
Further Approximation
Also, though still somewhat inaccurate, the quartertonal note B![]() is a better approximation for the seventh harmonic, since the eleventh harmonic is about a sixth of a whole tone lower than a typical B♭.
is a better approximation for the seventh harmonic, since the eleventh harmonic is about a sixth of a whole tone lower than a typical B♭.
The harmonic series can now be very reasonably approximated up to the twenty-fifth harmonic, which roughly splits the difference between G![]() and G♯:
and G♯:

Chords and Intervals
Since the seventh, eleventh, and thirteenth harmonics can be approximated with quartertonal notes, we can interface with the quartertonal notes while remaining in the tonality of a standard note. That is to say, the scale degrees ![]() 4,
4, ![]() 6, and
6, and ![]() 7 (or
7 (or ![]() 6) can, in a way, be considered harmonious since they approximate the harmonic ratios of 11:8, 13:8, and 7:4 in the same way that the standard major third approximates the 5:4 ratio.
6) can, in a way, be considered harmonious since they approximate the harmonic ratios of 11:8, 13:8, and 7:4 in the same way that the standard major third approximates the 5:4 ratio.
For example, this chord, which approximates harmonics 4 through 7, is used relatively often in the barbershop quartet harmonic vocabulary:
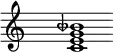
This chord can be further extended to include harmonics 9, 11, and 13:
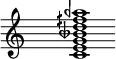
Extending Just Intonation
Historically, Western harmony only ever utilized intervals which approximated ratios involving prime numbers less than or equal to 5. This sort of tuning, referred to as 5-limit just intonation, prioritizes the use of harmonics 2, 3, 5, 9, etc., and not harmonics like 7, 11, and 13. Some composers utilized the seventh harmonic, but this was very rare and usually only with the intent of approximating Ancient Greek tonality.
The use of quarter tones allows—even if not perfectly—the use of ratios beyond those Western harmony utilizes. Even though Western-attuned ears may perceive quartertonal intervals as dissonances, there is, in fact, a just-intonation-based justification for almost all quartertonal intervals in some form when using higher forms of just intonation:
| Interval | Ratio(s) |
|---|---|
| 33:32 | |
| 13:12 | |
| 8:7, 7:6 | |
| 11:9 | |
| 9:7, 21:16 | |
| 11:8 | |
| 16:11 | |
| 14:9, 99:64 | |
| 13:8 | |
| 7:4 | |
| 11:6 | |
| 27:14 |